RESERVED
WITH THE RARE CANCEL T-P
(1) Sciographia, or the art of shadowes. Plainly demonstrating, out of the sphere, how to project both great and small circles, upon any plane whatsoever (2) Table des logarithmes, pour les nombres d’un, à 10000
(1) London, Thomas Harper, 1635 (2) Gouda, par Pierre Rammaseyn, 1626£3,750.00
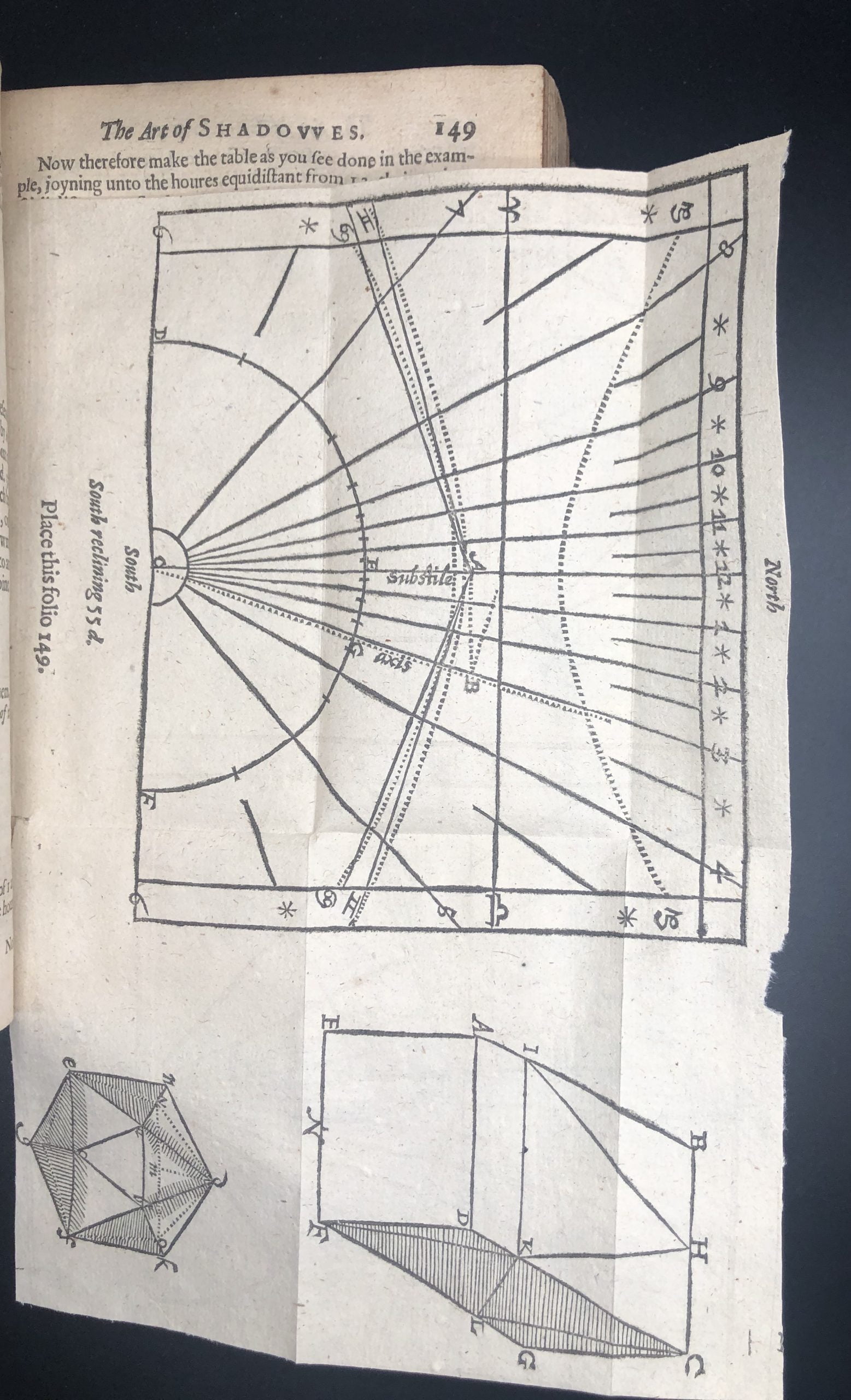
FIRST EDITION. Two works in one, separate title to each. 8vo. pp. [xlvi], 319, [lx], 380–427 (i): [par.] , A , 2a (-2a7,8), B-D , E , F-2E , 2F1(=a7), [2F]2(=a8). (2F1 and 2F2 inverted). Roman letter, some Italic. Floriated woodcut initials, woodcut headpieces, typographical ornaments, 13 folding woodcut plates, woodcut diagrams and illustrations in text, some full page, woodcut printers device on second title, slashed for cancellation in lower margin, two shelf marks in an early hand on pastedown, book labels of Harrison D. Horblit and Erwin Tomash above and below. Very light age yellowing, small hole, original paper flaw, in first C4 with loss of a few letters, closed tear in B5 with old repair in margin (perhaps original flaw repaired after printing). A very good copy, crisp and clean with all folding plates in immaculate condition, in contemporary English calf, covers bordered with a triple blind rule, rebacked, spine remounted, with gilt ruled raised bands, spine a little darkened, a.e.r.
Rare first edition of this important mathematical work, even rarer as the variant including the volume of Henry Briggs’s Table of logarithms. Wells wrote this book on dialling in 1622, when it was read by his friends Briggs and Gunter, who urged him to publish. A preface “To the Lover of the Mathematiques” was contributed by Henry Gellibrand. According to ESTC, this is a “variant” of Wells’s work “issued with unsold sheets of logarithmic tables by H. Briggs and A. Vlacq, published at Gouda by P. Rammaseyn, 1626”, the title of which is, unusually, present here though slashed for cancellation.
“John Wells was a London mathematician who specialized in the design of sundials. He was in close touch with the Gresham College mathematicians (Henry Briggs, Edmund Gunter and Henry Gellibrand) who worked with him on the more sophisticated issues that arose in designing accurate sundials, e.g., determining the correction needed due to variation of the compass, etc. In 1622, Wells wrote this book on dialing, which was so well regarded by Briggs and Gunter that they both urged him to publish it. Both men were particularly anxious to see it published because it represented a useful application of their newly calculated logarithmic tables (logs of numbers by Briggs and trigonometric logs by Gunter). Both Gresham professors died before this publication was accomplished, and it was at Henry Gellibrand’s urging that Wells finally published this work. Of course it was necessary to have a set of logarithm tables bound in with the book. Adriaan Vlacq had worked with Ezechiël de Decker to produce logarithms of the integers. These had been published prior to Vlacq’s famous 1628 tables. These tables had title pages in Dutch and French (and other languages). Unbound copies of these tables were obtained for binding with this volume. The plan was to bind them without their original title pages, and these were cut as a signal for the binder to discard them. This copy was accidentally bound with the cut title page (the French edition). Wells’ intention that the title page be omitted is supported by the fact that it makes no reference to the logarithms of the trigonometric functions that follow the decimal logarithms. These latter are set in a different type and do not appear to be from de Decker or Vlacq. A likely attribution is to Edmund Gunter because the log sin of 0º 30 min. is correct in this table (as it is in Gunter’s table of 1636 but is incorrect in Vlacq’s table of 1628). Further information may be found in Tracts for Computer, No. XIII, “Bibliotheca Tabularum Mathematicarum (Part I Logarithmic Tables)” by James Henderson, Cambridge University Press, 1926.” ‘Tomash, Williams, ‘The Erwin Tomash Library on the History of Computing. An Annotated and Illustrated Catalog” (This copy).
An excellent copy of this rare work.
In stock